二分查找（binary search），也称折半搜索，是一种在 有序数组 中 查找某一特定元素 的搜索算法。搜索过程从数组的中间元素开始，如果中间元素正好是要查找的元素，则搜索过程结束；如果某一特定元素大于或者小于中间元素，则在数组大于或小于中间元素的那一半中查找，而且跟开始一样从中间元素开始比较。如果在某一步骤数组为空，则代表找不到。这种搜索算法每一次比较都使搜索范围缩小一半。

时间复杂度:折半搜索每次把搜索区域减少一半，时间复杂度为O(log n)。（n代表集合中元素的个数）
空间复杂度: O(1)。虽以递归形式定义，但是尾递归，可改写为循环。

动图演示

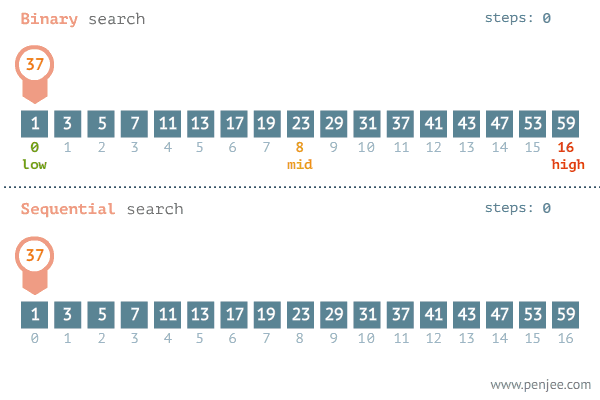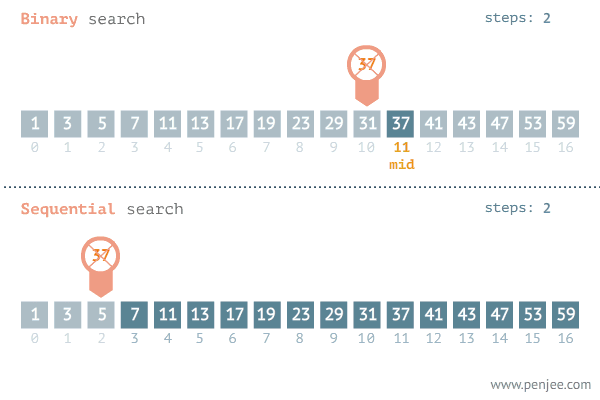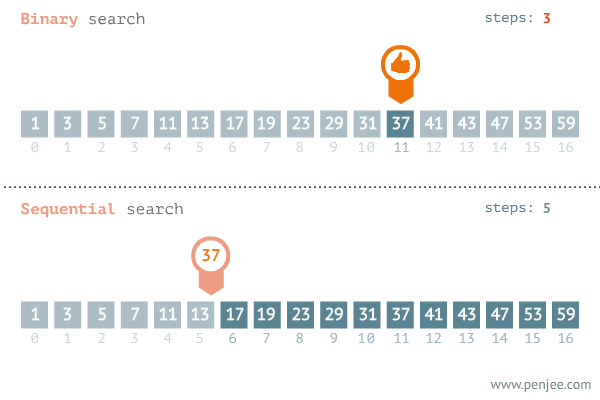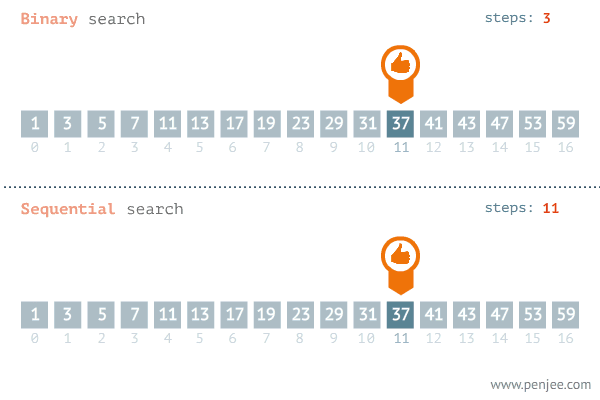
代码描述

递归

int binarysearch(int array[], int low, int high, int target) {
    if (low > high) return -1;
    int mid = low + (high - low) / 2;
    if (array[mid] > target)
        return binarysearch(array, low, mid - 1, target);
    if (array[mid] < target)
        return binarysearch(array, mid + 1, high, target);
    return mid;
}

非递归

int bsearchWithoutRecursion(int a[], int key) {
    int low = 0;
    int high = a.length - 1;
    while (low <= high) {
        int mid = low + (high - low) / 2;
        if (a[mid] > key)
            high = mid - 1;
        else if (a[mid] < key)
            low = mid + 1;
        else
            return mid;
    }
    return -1;
}

二分查找中值的计算

这是一个经典的话题，如何计算二分查找中的中值？大家一般给出了两种计算方法：

算法一： mid = (low + high) / 2
算法二： mid = low + (high – low)/2

乍看起来，算法一简洁，算法二提取之后，跟算法一没有什么区别。但是实际上，区别是存在的。算法一的做法，在极端情况下，(low + high)存在着溢出的风险，进而得到错误的mid结果，导致程序错误。而算法二能够保证计算出来的mid，一定大于low，小于high，不存在溢出的问题。

二分查找法的缺陷

二分查找法的O(log n)让它成为十分高效的算法。不过它的缺陷却也是那么明显的。就在它的限定之上：必须有序，我们很难保证我们的数组都是有序的。当然可以在构建数组的时候进行排序，可是又落到了第二个瓶颈上：它必须是数组。

数组读取效率是O(1)，可是它的插入和删除某个元素的效率却是O(n)。因而导致构建有序数组变成低效的事情。

解决这些缺陷问题更好的方法应该是使用二叉查找树了，最好自然是自平衡二叉查找树了，既能高效的（O(n log n)）构建有序元素集合，又能如同二分查找法一样快速（O(log n)）的搜寻目标数。

参考资料：